Batch 3 - Class 123 - Spider and the Ant
Pre-Class Problem:
There are 25 horses, but only one race track where 5 horses can race at a time. What is the minimum number of races required to determine the 3 fastest horses in order. Horses can be raced over and over again, and take the same time to run the track.
- Answer: 7. Race 5 groups of 5 horses each (5 races). Now race the winners of each race (6th race) - this gives the fastest horse. The next two fastest horses must be out of (a) the second and third from the initial race of the fastest horse; (b) the first and second from the 6th-race-runner-up's initial race; (c) Third horse from the 6th race. Race these 5 horses in the 7th race.
Attendance: Smiti, Muskaan, Tishyaa, Aneyaa, Arnav, Anishka, Anshi, Liza, Ahana, Palak, Manya, Diya, Arnav, Zorawar, Damini
Class Notes:
We have spider and we have an ant. They are sitting on a web. The spider wants to catch the ant! The web is a set of points, some connected and some not. Assume the ant is stationary, and the spider moves from one point to a random connected point. So in the square below, there are two equally likely choices for where the spider moves next. In the cube, there are three.
.png)
Instructor Notes: We may need to introduce the element of expected value. Take some simpler examples to illustrate that it is sum of (probability x outcome). For example, if I give you one rupee for heads and 10 rupees for tail, then the expected outcome is 5.5 rupees.
In this exercise, its important that kids can visualize the problem and the movements. Allow time for them to think through the paths, what possibilities exist. Younger kids may just be able to visualize the paths and might not be able to get to equations. Advanced kids should get to formulating the equations with some guidance.
- The web is a square as shown below left and the spider can visit each point only once. What is the average number of turns before the spider reaches the ant? How about the minimum and maximum?
- Answer: Note that the ant could be at any of the three remaining points (equally likely). The distance for spider to cover is 1, 2, and 3 units respectively. So average is 2.
- If the web is a cube as shown above at right, what is the average number then? How about the minimum and maximum number of turns?
- Answer: 1-7, average being 4
- Supposing that the spider can revisit points, what’s the answer for the square?
- Answer: 10/3. Couple of different ways of thinking about itWhat is the expected value to get to a point 1 distance away? Lets call this E1. One can reach that point directly, with probability 1/2. Or one can land up going the other direction, again with probability 1/2, and take (1+E2) steps in that case. So E1 = 1/2 + 1/2 (1+E2). Similarly E1 is 1+E1 (since the first step gets you to distance 1). If we solve for these, E1 = 3 and E2 = 4. Given that the ant is 1 distance away in 2 cases and 2 distance away in 1 case, overall expectation is (2E1+E2)/3Alternately, lets try to consider all ways of reaching point one distance away. First, there is a direct path with probability 1/2. Then there are paths of length 3, where the first move has to be the opposite point (probability 1/2), second can be anything (probability 1), and third has to be to the destination (probability 1/2). So, the expected contribution is 3 (1/2.1/2). Similarly, contribution of distance 5 is 5 (1/2.1/2.1/2) and so on. Sum this infinite series, and we get E1=3. Similarly, we get to E2=4
- How about for the cube? And do the minimum or maximum numbers change?
- Answer: 58/3 (E1=7, E2=9, E3=10) - solution similar to above. Minimum is 1, Maximum is infinity
- What if the spider starts at 1 and the ant at 0 on the number line? Or in 2D?
- Answer: We can follow the second approach. Distance 1 probability is 1/2. Distance 3 probability is 1 x 1/8. Distance 5 probability is 2 cases x 1/32=1/16. Distance 7 probability is 5 cases x 1/128=5/128, and so on. Sum the series.What if the Ant was at 0 and Spider was at 2?Ask kids to think about the 2-D problem.
Homework
(Dudeney - 230) Here is a pretty little puzzle that only requires twelve pennies or counters. Arrange them in a circle, as shown in the illustration. Now take up one penny at a time and, passing it over two pennies, place it on the third penny. Then take up another single penny and do the same thing, and so on, until, in six such moves, you have the coins in six pairs in the positions 1, 2, 3, 4, 5, 6. You can move in either direction round the circle at every play, and it does not matter whether the two jumped over are separate or a pair.
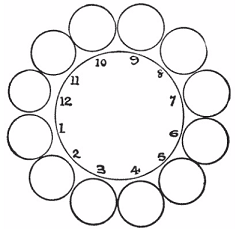
- Answer: 12->3, 7->4, 10->6, 8->1, 9->5, 11->2
- What if we wanted them to jump two stacks of pennies, regardless of number of pennies in that stack?
- Answer: 10->1, 9->6, 11->2, 8->5, 12->3, 7->4
References:
https://ia902701.us.archive.org/4/items/AmusementsInMathematicspdf/AmusementsInMathematics.pdf - Dudeney
Unused elements
- Is there a path that the spider can follow so that he will visit each point exactly once?
- Answer: Yes for both shapes
- How about each edge (connection) exactly once?
- Answer: Note that we have done the test for each edge being visited once - it has to have 0 or 2 vertices with odd numbers. So its possible in square but not in cube
- What about each edge and point exactly once?
- Answer: No. Clearly for this, you need a straight line formation
- Try the same problems for an octahedron (8 faces, 4 edges from each point), icosahedron (20 faces, 5 edges from each point) or a dodecahedron (12 faces, 3 edges from each point).
- Instructor Notes: Kids should be able to think this through and formulate the equations. May be advanced kids
- What if the ant is also able to move at random?
- Instructor: Focus on whether kids can formulate the problem in terms of equation.